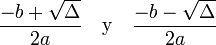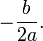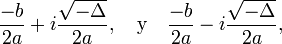Función cuadrática,¿dónde estás?
Funciones CuadráTicas from María Elisa Gassmann
y ahora a empezar con este desafío!!!
Para guiarnos en lo que sería algunos de los temás a tratar, lo hacemos a partir del mapa conceptual:
lunes, 7 de julio de 2014
Función cuadrática
FUNCIÓN
CUADRÁTICA
La función cuadrática, surge como una
contribución árabe cerca del año 700 y 1200 d C. en la época llamada “Edad de
Oro”. Hace clic e Investiguemos:
Y
lo más sorprendente de las funciones cuadrática es donde la podemos encontrar. Descubridlo!!!
En
matemática una función cuadrática o función de segundo grado, es una función
polinómica que se define mediante un polinomio de segundo grado como:
Donde a, b, c son números reales y a es
distinto de cero
La representación gráfica en el
plano XY haciendo:
Esto
es: 
Cuya concavidad depende del coeficiente
principal “a”, la cual puede ser :
En cuanto a su intersección con los ejes del
plano cartesiano
Las intersecciones con
los ejes del plano cartesiano XY, están dadas por las siguientes condiciones y
fórmulas:
! EJE “X”:
1
|
Sí
Δ > 0
|
Interseca
al eje x en 2 puntos,
 |
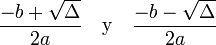
2
|
Sí Δ= 0
|
Interseca
al eje x en un punto,
 |
3
|
No hay intersección con el eje
x
las raices son:  |
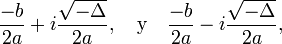
Y
para hallarlas, será necesario reemplazar los valores de los coeficientes
en la fórmula resolvente:
! EJE “Y” : La
intersección con el eje y, corresponde al par ordenado (0;c)
EJE DE SIMETRÍA DE LA FUNCIÓN
CUADRÁTICA
El eje de simetría de una
parábola es una recta que divide simétricamente a la curva, es decir,
intuitivamente la separa en dos partes congruentes. Puede ser entendido como un
espejo que refleja la mitad de la parábola en cuestión.
La
ecuación asociada al eje de simetría viene dada por la relación: 
MONOTONÍA Y ÁMBITO DE LA
FUNCIÓN CUADRÁTICA
La representación
de las funciones cuadráticas es siempre una parábola con eje de simetría
paralelo al eje de ordenadas, que la divide en dos ramas, una creciente y otra
decreciente.
VEAMOS ALGUNOS EJERCICIOS
¿Te animas?
Suscribirse a:
Entradas (Atom)